Improving the bottom line: reducing the cost of compressed air

The cost of compressed air continues to be a very elusive subject in industrial applications. The notion that compressed air is free is a common misconception.

Countless attempts at making end users aware of the costs to produce compressed air have largely been ignored. It seems that operations managers are concerned with the power consumption of a couple of 60 W light bulbs, but couldn’t care less about the power required to run a 400 hp compressor. Let’s put this into perspective - one horsepower equals 745.7 W. You can light 4971 light bulbs with the same power it takes to run a 300 kW compressor. Indeed, the single largest electrical appliance in a manufacturing plant may be the compressor motor.

Compressed air costs are typically hidden in the operating overheads of most companies, therefore any overhead cost reduction immediately falls to the bottom line in the form of profit. The real test of this improved bottom line is determining the additional sales a company must generate to produce a similar profit.

Real costs

Experts in the compressed air field suggest the cost to produce compressed air varies from $0.15 to $0.40 per 1000 standard cubic feet (SCF)^1,2, depending on geographical location. In spite of these estimates, a large sector of the user public fails to complete the simple calculations to determine what a machine will require in terms of standard cubic feet per minute (SCFM) of compressed air, let alone for an entire year or the life of the equipment. In order to improve the bottom line with pneumatics, we must also expose three popular pneumatic myths:

• Myth 1: Compressed air is free
• Myth 2: Pipe size = Right size
• Myth 3: If a little bit’s good, a whole lot’s better

Myth 1: Compressed air is free

In the past most people wouldn’t take the time to determine the cost of the compressed air required by an actuator for a year. It is ironic that hydraulic system designers have to do the calculations in order to determine the size of the power unit required to operate hydraulic cylinders. For far too long, little effort has been made to recognise the similarities between hydraulic and pneumatic systems. Typically, fluid power people have defended the differences between hydraulic and pneumatic systems. By recognising the similarities we can design and service the two mediums from similar perspectives, including the need for safety, conservation, component sizing and cost justification.

There is a developing interest in determining the cost of compressed air in a pneumatic system. We are beginning to see users specify 60 psig as the maximum pressure range for a pneumatic system. Pneumatic component manufacturers are somewhat paranoid about discussing the cost of compressed air for fear they might encourage customers to apply a substitute for compressed air. Since compressed air is readily available, affordable, clean and has less force hazards than hydraulic power, it seems reasonable that compressed air will continue to be applied in the industrial sector.

Real common sense

To properly apply pneumatic components in a system, the first component to be considered is the actuator. We have seen a large number of cylinders grossly oversized resulting in poor actuator performance, wasted compressed air and high initial component costs. Oversizing an actuator by one bore size can result in a 50% increase in the cost of compressed air required for the application. If the cylinder is sized to move more than twice the load at the design pressure, the cylinder speed will be adversely affected and the cost of compressed air will also increase. Using this simple observation can result in significant savings.

If care is taken at this step of the design process, every component upstream of the actuator (valves, conductors, fittings, filters, regulators and lubricators) will have a better chance of being correctly sized and applied. A good and correct start in the process is essential to having an efficient system.

Real calculations

A cylinder flow calculation is required for a number of reasons. It takes into consideration the force required to move the load at the specified pressure, the extend and retract stroke volumes of the cylinder, the cycles per minute, the operating air pressure and a conversion to  SCFM. SCFM is the value used by most pneumatic fluid power manufacturers to apply the correct components in a system. SCFM is also linked to valve sizing using the flow coefficient (C_v).

Once the cylinder flow calculation is completed, the designer can determine the correct tubing, fittings, valves and the filter, regulator and lubricator (FRL) for the application. In spite of the obvious benefits this information provides, we find few designers attempting these critical calculations.

Figure 1: Typical valve/cylinder/flow control circuit.

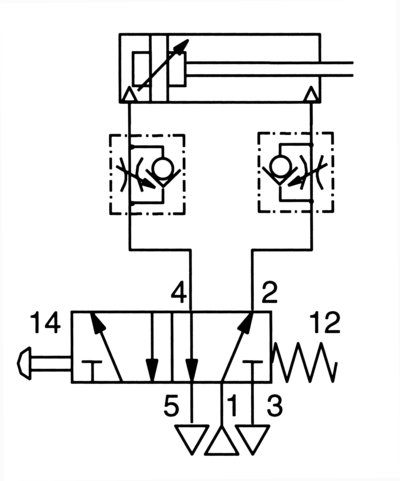
In a typical circuit (Figure 1) comprising a double-acting pneumatic cylinder, a five-port, four-way valve and two flow controls, the typical approach to sizing exposes another popular pneumatic myth.

Myth 2: Pipe size = Right size

If the cylinder selected had a 1/2″ pipe port, most installers would apply 1/2″ flow controls, 1/2″ pipe and fittings, a 1/2″ valve and, quite possibly, a 1/2″ FRL! This approach leads to oversized, high-priced components and higher long-term operating compressed air costs over the life of the equipment. As a result, oversizing components occurs frequently and quickly leads to another popular pneumatic myth.

Real-life example

Let’s consider the following example. We have a cylinder load that requires 2.2 kN of force to move in the extend direction only. The retract stroke has no effective load. We want to move the load 30 cm and be able to do this at 30 cycles per minute, eight hours per day, five days per week, 50 weeks per year. The cylinder will be operated on a horizontal plane. Compressed air pressure is 80 psig (552 kPa). Of course, we want this cylinder to move as fast as possible (AFAP)!

Real solution

There are five steps required to accurately calculate a cylinder flow rate (in SCFM). The calculations are necessary to achieve accurate results. After the calculations are completed the system designer has the information needed to make sound, cost-effective decisions that include downsizing components and conserving compressed air.

Step 1: Size the cylinder for maximum performance

This is the stage in sizing a cylinder where we find many designers throwing in a little extra safety factor to cover breakaway forces of a cylinder (if a little bit’s good, a whole lot’s better!)

Based on common practice and the orientation of the cylinder, we have found the range of the force multiplier to be between 1.25 to 2 times the load³ being moved, at the specified pressure. This range of values will provide adequate force compensation in the calculations and need not be exceeded.

To size the cylinder for maximum performance (quickest stroke time) we will apply the x2 rule. Multiply the load by two and apply the correct cylinder at the specified pressure. In this case, 2.2 kN x 2 = 4.4 kN. Using the formula, force is equal to pressure times area (f=pA), we solve for the cross-sectional area we need for the cylinder bore. To solve for the area, the formula looks like A=f/p. 4.4/552= 0.008 m² = 80 cm² is the cross-sectional area of the bore needed to move our 2.2 kN load as fast as possible! This is very close to a standard ISO bore of 100 mm (78.5 cm²). It is IMPORTANT to note here that any larger bore size will move slower at 80 psig and any smaller bore size will also move slower. Use a 100 mm bore cylinder.

Step 2: Calculate total volume per cycle

Total volume per cycle requires some examination of the cylinder we will be applying. We need to recognise that the extend stroke volume will be more than the retract stroke volume on a typical double-acting, single-rod cylinder, due to the volume displacement of the rod.

Since we’ve selected an ISO 100 mm bore cylinder we will apply the standard 25 mm rod (after we’ve checked to avoid cylinder rod buckling!). Extend volume is equal to the bore cross-sectional area times the stroke length.

   78.5 cm² x 30 cm = 2355 cm³

Retract volume (compensating for the rod) calculation is:

   (78.5 cm² – 4.9 cm²) x 30 cm = 2208 cm³

Total volume per cycle is therefore:

   2355 cm³ + 2208 cm³ = 4563 cm³

For a 125 mm bore the total volume per cycle is:

   3681 cm³ + 3440 cm³ = 7121 cm³

That’s a 56% increase over the volume of the 100 mm bore cylinder!

Step 3: Calculate total volume per minute

Multiply the total volume per cycle by the number of cycles per minute:

   4563 cm³/cycle x 30 cpm = 136,890 cm³/min

Step 4: Convert to cubic feet/minute (CFM)

   136,890 cm³ ÷ 16.387 cm³/in³ ÷ 1728 in³/ft³ = 4.83 CFM

Step 5: Convert CFM to SCFM

This conversion reduces the cylinder flow calculation to the necessary and required terms.

To make this conversion we must recognise the compression ratio of the compressed air being used in the application. Compression ratio is the working pressure expressed in absolute terms and converts compressed air to standard conditions (14.7 psia, 36% RH and 20ºC temperature). In most industrial applications, the ambient temperature and relative humidity can be ignored since these variables have little impact on the calculations.

Our compression ratio (CR) calculation is:

   (80 + 14.7) ÷ 14.7 = 6.44

Multiplying the CFM by the CR = SCFM:

   4.83 CFM x 6.44 CR = 31.1 SCFM

An SCFM of 31.1 for this application seems fairly harmless until you complete the compressed air cost evaluation. The cylinder flow calculation provides the necessary information (SCFM) to more accurately determine the flow coefficient (C_v) and the proper FRL for the system. Without the cylinder flow calculation, sizing the rest of the components in the system will be accomplished empirically (trial and error approach) or by using Myth 2.

With the cylinder flow calculation complete, we can move on to the real cost of compressed air for the application and sizing the rest of the components in the system.

Real power requirements

Most compressor representatives will use a few rules of thumb to determine the compressor capacity required for an application. Depending on the type of compressor used, compressors are typically rated to deliver four to five SCFM per horsepower as a rule of thumb. Most compressor representatives will also strongly recommend a duty cycle of 50% to 75% (rule of thumb), again depending on the type of compressor. Duty cycle is the percentage of time the compressor motor is generally running under loaded conditions. In our application, at 50% duty cycle and at 4 SCFM/hp, a 31.1 SCFM application will require an additional compressor capacity of 11.6 kW! (31.1 SCFM ÷ 4 SCFM/hp) ÷ 50% duty cycle = 15.55 hp (11.6 kW).

Real compressed air costs

If we carry our SCFM calculations out to the number of SCF per year, per shift, pretty soon we are talking about some serious compressed air usage! Consider how many minutes there are in an eight-hour day, five days a week, fifty weeks in a year: 120,000 min/year per eight-hour shift (That’s 360,000 min/year for three shifts!)

   31.1 SCFM x 120,000 min = 3,732,000 SCF/yr.

The 125 mm bore cylinder would require 48.5 SCFM or 5,820,000 SCF/yr. If your average cost per 1000 SCF is only $0.25, the cost of compressed air to operate this one 100 mm bore cylinder for one shift, for the year is an incredible $933, and obviously, if your cost of compressed air is $0.50/1000 SCF, your annual cost would be $1866.00.

For the 125 mm bore, air consumption costs jump to $1455 (at $0.25/1000 SCF) and $2910 (at $0.50/1000 SCF). Over a 55% increase for one bore size increase.

Real concern

The cost of compressed air actually used is a major concern for most manufacturing companies. If we could reduce the compressed air consumption in our system by 30%, most CEOs, CFOs and plant engineers would leap at the opportunity. Let’s consider another approach to our application.

Since our 2.2 kN load is only being moved in the extend direction, we could consider lowering the air pressure to return the cylinder. For example, say we were able to lower the return pressure from 80 to 20 psig. How would that impact on the total system air consumption?

If you recall from Step 2 above, the retract stroke volume was 2208 cm³ per cycle, or about 48.4% of the total cycle volume. Without taking you through the additional calculations, the compressed air cost for the extend stroke at $.25/1000SCF is (51.6% of $933) $481.43/year.

Again, without going through the calculations, it can be shown that by changing the pressure on the return stroke to 20 psig the compressed air consumption is reduced by 30%, therefore saving 30% in compressed air costs overall for this actuator.

Even if the price of a 1/2″ regulator was $50, you would be able to expect a payback on the cost of the regulator in about two months.

Please keep in mind this example is for only one 100 mm cylinder. How many cylinders are you applying? What is your cost of compressed air?

When we examine the application even closer, we are able to save even more in initial costs by properly sizing the valve, the fittings and tubing by the use of the flow coefficient (C_v). It is sufficient to say the use of C_vs to size a system is reasonably accurate and provides an element of cushion in most system calculations.

There are other approaches to conserving compressed air in typical applications. If cylinder speed is not important, using a force multiplier between 1.25 and 2 times the load will result in smaller cylinders and less air consumption. Applying single-acting cylinders could significantly reduce the long-term cost of compressed air.

Real system C_v

Using C_vs we can evaluate the typical circuit of Figure 1 for potential bottlenecks. Each component in the circuit has a C_v. With some effort it is possible to determine the C_v of the cylinder port, C_v of the flow control (in both the free flow direction as well as the WIDE OPEN controlled flow direction), C_v of the piping/tubing and fittings and the C_v of the directional control valve. The System C_v is ALWAYS going to be less than the component with the smallest C_v in the system.

A strong recommendation here is to make the most restrictive component (‘the weakest link’)⁴ in the system the most expensive component (usually the directional control valve). This will minimise the initial cost of the components in the system. It is fair to say that a 1/2″ directional valve will cost more than a 1/4″ valve. The difference in pipe or tubing cost is marginally different.

Real savings

With dual pressure savings, you can see the fast payback on applying additional regulators. More impressive savings can be realised by finding the leaks in the compressed air system and eliminating them. We have seen reports suggesting compressed air losses due to system leaks and artificial demand range from 20 to 45%!⁵

Compressed air leaks, left unattended, will continue to grow in size and flow due to the abrasive effect of the air-line contamination and particulate matter continuing to attack the leak orifice.⁶ The sooner leaks are discovered and repaired, the less waste there is in power required to produce the compressed air. Less wasted air reduces operating costs and can justify the expense of a maintenance patrol to quickly repair air leaks.

Real maintenance

After all of this discussion to reduce the operating costs associated with wasting compressed air, we must mention another, less obvious, source of waste. Users should regularly check for excess pressure drop across air filters. By applying pressure drop indicators (also called service life indicators or delta P indicators) and changing filter elements with greater frequency, you will avoid the escalating cost of the pressure drop across the filter element. Electronic and mechanical pressure drop indicators are commercially available to provide reminders to service the filter elements on a regular basis. Using pressure switches to monitor regulated pressure in the system will avoid surpassing the x2 multiplier, ensure efficient use of compressed air and provide optimum performance of the system.

In hydraulic systems, a pressure drop across a filter has serious consequences affecting the entire hydraulic power unit adversely. Poor maintenance on hydraulic filters results in catastrophic failures. In hydraulic systems, leaks are quickly repaired due to the obvious hazards and cost associated with hydraulic oil. Rarely does poor maintenance on a pneumatic filter result in catastrophic failure. However, excessive pressure drop across a pneumatic filter is an ongoing operating cost that is hidden from view. In pneumatic systems, leaks are often ignored until they become so annoying (uncomfortably loud), or they have caused such a significant system pressure drop, that they must be repaired.

Summary

If you don’t care about the cost of compressed air in your plant, don’t do the calculations, and you will perpetuate the three pneumatic myths! Consider the similarities between pneumatic and hydraulic systems, rather than the differences.

If increased profits are of interest to you, then you’ll find a hidden profit centre in the cost-effective use of compressed air. If you reduce your compressed air overhead costs, avoid oversizing components and design your systems to operate at an optimum pressure, you can improve system performance and improve the bottom line. The first step to recognising the potential savings available to you is completing these simple calculations.

With a little time and effort, you can make a big improvement on your bottom line with pneumatics.

References

1. Electric Power Research Institute 1994, Compressed Air Handbook, Electric Power Research Institute, p12.
2. Wagner, HH 1999, ‘Your Total Compressor Cost May Be Too High’, Plant Engineering, May 1999.
3. Fleischer, H 1999, ‘Stop Oversizing Pneumatic Components’, Machine Design, June 1999, pp 101-106.
4. Fleischer, H 1995, Manual of Pneumatic Systems Optimization, 1st edn, McGraw-Hill, New York, 1995, pp 25-66.
5. Foss, RS 1998, ‘Improving Air System Efficiency Part 1’, Hydraulics & Pneumatics, April 1998, pp 41-68.
6. Foss, RS 1999, ‘Improving Air System Efficiency Part 7’, Hydraulics & Pneumatics, July 1999, pp 33-79.